This is a translated and adopted article I wrote for the Aha'22 (30 May 2022) conference. It describes an approach to a marketplace prices optimization. I am working on price optimization in Yandex Market and I am going to share the most important ideas and components that we have developed to solve the task. Previously, I was engaged in projects related to Machine Learning (ML) in advertising technologies, and a year ago the topic of pricing was completely new to me. As a newbie entering a new field, It was natural for me to systematize state-of-the-art concepts and ideas. And, you know, the best way to do it is to write an article about it. So here I've outlined some important definitions and tried to define the scopes and roles of ML, algorithms, and humans in optimal pricing. Although the article covers rather basic things you can find out some new formulas and ideas, because the mentioned state-of-the-art concepts are somewhat "well-known only in a very closed clubs", and besides, the real gem found here is the detailed recipe for ML engineers how to build optimal pricing systems. The approach I propose here is simplified in that it is based exclusively on independent demand curves. However, I hope it will be interesting and useful to someone.
Please, do not hesitate to share your thoughts in the comments.
A small disclaimer. Yandex Market is a marketplace where tens of thousands of sellers can list their products. Sellers decide for themselves which products to sell and at what prices. But, among being aggregator, Yandex Market itself acts as one of such sellers. Thus, Yandex Market has the opportunity to set prices for some goods, and it is the optimal pricing for these exact goods that we are discussing here.
What are the demand curve and price elasticity?
The demand curve expresses how demand depends on price. The lower the price, the higher the demand, and vice versa.
Once you have the demand curve for a particular product, you can use it to develop pricing strategies. Given a specific business goal, optimal prices can be derived from the demand curves. Most businesses aim for profit, therefore the task is formulated as
Given demand curves for all goods, calculate prices that maximize profit.
We have to mention some issues that immediately pop up in the heads of experienced trade marketers:
How to get these curves? There are a number of difficulties:
There are too many goods, thousands, or even millions.
The curves change over time.
Sometimes, curves are stepwise, with steps at competitors' prices, so you need to monitor these prices, and this is a rather complex task requiring constant attention. Competitors may have differing delivery terms, warranty periods, production dates, and levels of support service. And you have to take this into account while comparing prices.
The demand for a good depends not only on its price, but also on the prices of related goods. You can attract buyers with discounts on one set of goods, and sales will rise for an extended set of goods.
The task is not solely to maximize profit. There are a number of additional aspects of pricing strategy:
Consideration of the cumulative price perception of all products
Market capture, i.e., not only is profit important, but also total turnover
Taking into account expiration dates
Consideration for the sale of obsolete models
Management of 'dead stock', i.e. items that have not sold for an extended period and seem unlikely to sell at the current price
The Yandex Market pricing team addresses some of these issues while working on automation of pricing. In this article, we only cover some aspects:
ML for predicting demand curves, including features, targets, and Python + PyTorch code samples
The balance between profit and market capture (GMV), including the underlying mathematics and simple formulas
The optimal pricing algorithm
Are there any state-of-the-art ML approaches for pricing?
Price Elasticity prediction and Price Optimization are undoubtedly of core importance for market-related businesses, and as any complex task on the edge of technology and human expertise, they start incurring great influence from Machine Learning community. One can find many calls to power market pricing with ML:
Machine Learning for Retail Price Optimization: The Price is Right
Using machine learning algorithms to optimize the pricing process is a must for pricing teams of mature retailers with at least thousands of products to reprice regularly. As the technology is gaining popularity in the industry, the ability to manage ML-powered software will soon be an indispensable part of a pricing or category manager’s job description. There’s simply no way around it, as it gives pricing managers the unprecedented level of precision and speed of decision-making across any number of products.
Erik Rodenberg, CEO, Black Wave Consulting Group
Price optimization notebook for apparel retail using Google Vertex AI
The product prices often change based on the observed market response, sell-through rates, supply disruptions, and other factors. Rule based or manual price management in spreadsheets doesn’t scale well to large catalogs with thousands of items. These methods are slow, error prone and can often lead to inventory build up or substantial revenue losses. Machine Learning methods are both faster and provide more formal optimality guarantees. These models can significantly improve the productivity of human experts by allowing them to automate large parts of their decision making process
However, this calls do not refer to any existing state-of-the-art frameworks for building ML-powered automatic pricing software (ML AP).
The video "How to build ML pricing systems" at Karpov.Courses is a good step towards understanding the role of ML in AP, but it does not fully describe the framework and details, while these details are crucial to make ML AP work.
Furthermore, the availability of tutorial materials on optimal pricing leaves much to be desired. Just try to find any printed or online materials describing and explaining the following basic formulas for optimal prices:
These prices maximize profit and lagrangian for the standard price elasticity model when demand is proportional to
. This demand curve corresponds to the case of constant point elasticity equal to s.
So, our first goal here is to fill this gap, and describe how method of Lagrange multipliers is used when optimizing for balance between GMV and profit. We will derive mentioned basic formulas and explain intuition behind them. In our opinion, these formulas should be on the Wikipedia pages, because they are rather simple and clearly demonstrate common trade-off between GMV and Profit. Although these formulas are derived for a special case of the demand curve, they still provide important insights into optimal pricing. We speculate that most pricing teams in global marketplaces are aware of these formulas but either don't consider them worth publishing or, on the contrary, view them as part of their intellectual property.
Nonetheless, we hope this article and our report at Aho'22 will fill the gap in publicly available information about simple demand curve-based pricing strategies.
It is believed that optimal pricing strategies are complex, require expertise and could not be moved to full automation. Some companies sell expertise of setting optimal prices for substantial budgets and some buy that expertise. But where does the complexity of building automated pricing platform lay? Is it possible to hire a recent graduate with ML skills that will accomplish this task for you in few months. Let's figure it out.
Demand curve samples
It's worth introducing normalized demand curves, i.e. function E(r) of relative price
r = price / price0,
equal to demand multiplier.
So, if demand for price0 equal to demand0, then demand for the new price is
demand0 · E(price / price0)
One can write definition like this:
One option for price0 is the average price for last N weeks. There are other valid options, such as the minimum competitors price or average purchase price. We advise considering them all and measuring the stability and quality of different options via AB-testing. Generally, the function E(r) depends on the price0 choice. However, there is a unique parametric demand curve family for which choice of price0 does not affect E(r):
Let's call this the power curves family. Our research has shown that for majority of goods we are fortunate to have demand curves close to curves from this family when the price is in the segment .
Hear we provide one example of a power curve with :
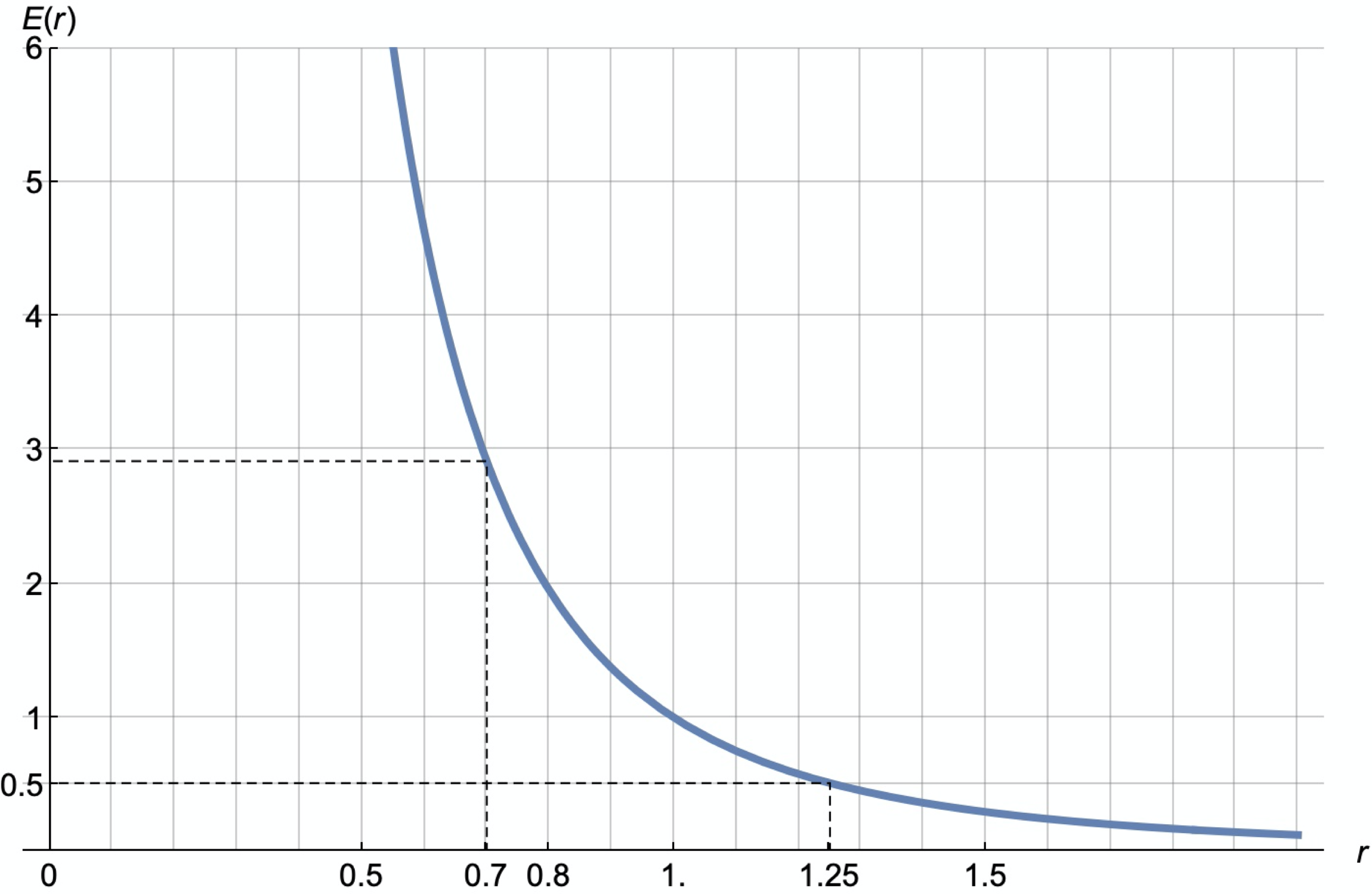
In this case, we see about a threefold increase in demand at a discount of about 30% (r = 0.7), and a drop of about 2 times with an increase of 25% (r = 1.25).
Here are examples of E(r) curves for some products sold on Yandex Market. They were inferred via neural networks implemented in PyTorch.


The first plot is represented on normal axes, and the second one is on logarithmic axes.
A power curve on logarithmic axes looks like a straight line. As can be seen, some demand curves on logarithmic scale resemble straight lines, others curve downwards (convex down), and others curve upwards (convex up). Consequently, we will refer to these curves as power-law (navy), sup-power (yellow), and sub-power (light green). And some curves are difficult to attribute to one of these three classes (light blue).
How to "read" a demand curve
As can be seen, for different goods, a 30% discount can increase sales by 3, 5, 10 or even 50 times. The yellow curve in the plot above is "a tea", that is, a good
bought by many (a product-for-all)
bought regularly
with a well-known price
and it's price is easily compared to prices in other marketplaces.
Let's draw this curve separately in navy-blue on logarithmic scale:

Feature properties of this curve include:
The steepest slope is near r = 0.8, that is 20% discount. At this point we encounter the competitor's price.
It is a hero-product – we can increase demand by 50 times.
It exhibits low elasticity for small discounts – it's inexpensive, and a user is unlikely to switch marketplaces for a mere $0.1 price difference.
The Slope
The first important characteristic of a normalized demand curve E(r) is the slope at r = 1. Let's denote it as slope or simply s. It is equal to Price Elasticity for small changes in price.
For instance, a slope of 4 signifies that demand grows by 4% when the price is decreased by 1%.
The slope provides information about exchange rate of relative price to relative demand only in the vicinity of the point r = 1. Function E(r) for "a tee" exhibits small slope in the vicinity of r = 1, but grows dramatically up to 12 near r = 0.8.
There are four basic variants of analytical normalized demand curves: linear, exponential, power, and hyperbolic:
Let's draw them with same slope = 3:
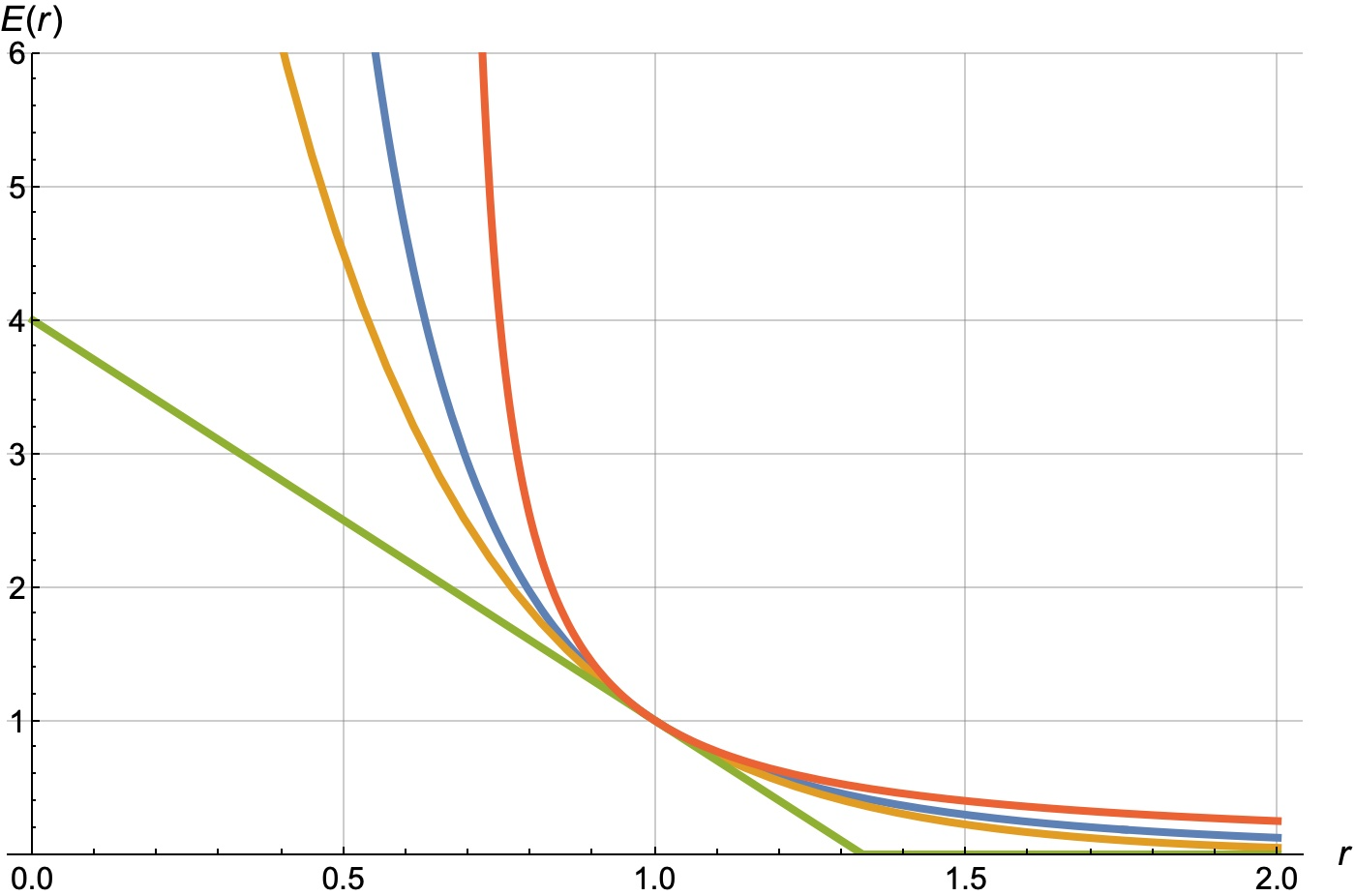
green – linear, yellow – exponential, navy blue – power, red – hyperbolic.
See formulas for optimal prices for these four families in the next section.
Now, let's discuss the main factors that affect the slope.
Basic elasticity: This isn't a factor per se, but an intrinsic property of a good. It characterizes the demand curve for a typical price under standard conditions.
The expectation of discounts: There are factors that can alter this Basic Elasticity. For instance, retail events like Black Friday or holidays can not only shift the demand but also modify the elasticity. Retail occasions and holidays make discounts expected and increase the natural reaction to discounts.
Visibility of discounts: It's crucial for discounts to be clearly visible. These are coloured price tags, crossed old price, various markers on product cards in online stores. You can have special promo blocks in the mobile app and on the website. In addition you can have a special ranking in the feeds with boost of products having discounts.
Clarity of discounts: For promo codes and various coupons, the clarity of conditions for applicability, the size of the discount, and the simplicity of application are also critically important.
Basic elasticity could also be broken down into several factors such as category, demand class, price class, whether the product is well-known or not, and whether it's new or has been known for a long time. There are many other product properties, and the concept is to incorporate these properties as input features into the ML model so that it can deduce basic elasticity from these properties.
Other three factors are about promotion mechanics (or, in short, promo) itself and the main takeover here is:
Price elasticity of a product is not a constant, it's something you can change via promo expectations, visibility and clarity.
Here, we need a close collaboration between marketers and ML engineers. They should develop strategies on how to measure and predict the effects of various promos on price elasticity. These properties could include: the start date, duration, promo type (cashback, promo code, or just drop in price), minimum basket size, whether promo applies to all assortments or only certain subcategories, etc. The next step involves determining how to construct the most effective promo, and this is the topic for the next article.
Yandex Market Dynamic Pricing Vocabulary
Developing your own vocabulary is a good thing to have. Apart from being fun, it allows you to be more concise and expressive, and somehow, could level up your team work.
First of all, we can name some slope-classes:
low elasticity: slope ≤ 2
normal elasticity: 2 < slope ≤ 4
high elasticity: 4 < slope ≤ 10
super elasticity: slope > 10
You can also define Slope as function of r:
In the context of machine learning pricing for marketplaces, there are several specific terms that help engineers and marketers understand each other better, set objectives more formally, and translate marketers' requirements into technical specifications for specific classifiers and formulas for ranking goods.
steep point: Point in the vicinity of which the demand curve has a large slope. This point is usually an inflection point on a log-log-scale plot and is typically located near a competitor's price.
tee-goods: Insensitivity to small discounts. Goods with slope < 2 in the segment [0.9, 1.1], but at the same time demand grows at large discounts, so that Slope(r) > 4 for r < 0.8.
cup-goods: Highly competitive goods. Goods that have many analogues in your store or in other stores.
locomotives: Goods whose sales growth leads to sales growth of N other fixed goods (N wagons), for example phones and accessories to them.
magnets: Goods whose sales growth leads to an increase in sales of many other goods; customers come to the store for them, and often they are the first goods in the basket;
basket-starters: Goods that are most likely to be put in the basket first.
ubiquitous goods: Goods that are available in many stores.
universal goods: Goods that will be bought by more than 30% of users if you give a 50% discount.
dwarf goods: Goods with limited growth potential. Goods which sales stops growing after reaching a certain discount value. Demand for such good is limited, because only small percentage of population are ready to buy it for any price.
Using these specific terms, engineers can train predictors such as
E(r),
probability that E(0.7) > 10
"locomotiveness"
"magnetism"
probability that the user will compare the price of this product with the price in the competing store
percentage of users who would buy this product if a random user were offered a 50% discount on the main storefront
These predictors can then be used to select and rank products, for example for identifying top KVIs.
KVIs (Key Value Items) are items in product assortment, that drives the value/price perception of a retailer by customers. If you break this down into basic components, you get items that are highly elastic goods, basket goods, magnetic goods, common items, and regularly purchased items.
By using five corresponding predictors, an engineer can create a measure of a product's KVI-ness.
Another example is a hero good, which can be defined as a combination of properties:
universal
highly magnetic
with E(0.7) > 30
Hero items are ideal for major promotional campaigns with media support and for featuring on the main storefront.
In this way, having a set of basic predictors, you can generate lists of products for various promotional activities or pricing strategies by blending basic predictors, combining inputs and ideas from both the marketers and the engineers.
Training demand curve
Measures of a good's "KVI-ness" or "heroism" are certainly of great importance, but the basic thing in optimal pricing is the demand curve E(r) for each good. And the important message of this article is that these curves can be trained using ML, and particularly Neural Networks.
The concept of "training the demand curve" may sound bizarre to some. How can you train a demand curve? Demand curve is the curve that one can explore simply by setting different prices for the same product at different times or in different stores.
But the very important thing here is that "you can't simply explore demand curves". And this is the bad news. It is practically unfeasible to obtain demand curves for products by trying different prices due to limited time and a lack of stable periods for sales for week to week comparison. It is necessary to somehow extract/generalize information from the natural movements of prices and sales in the past.
In the past prices fluctuated, and there is a challenge of extracting signal about elasticity from historical data. One can also intentionally randomly "wiggle" the prices to get information about demand at different prices. This "random wiggling" is called exploration. We did not do this, and it seems that in our case, the natural historical data is sufficient to obtain an acceptable result.
Products can be similar in various aspects, such as category, brand, price range, popularity, color, and other characteristics. Thus, even if the price of a specific product has remained the same or changed minimally, it's possible that similar products exist, and their demand curves can be "inherited". These similarity aspects gives us a chance of using historical data on different similar products for mutual enrichment and ultimately deriving the demand curve for any product based on its properties.
The good news is that today, there are a well-developed and actively evolving Machine Learning (ML) algorithms and technologies with ready to use tools for working with data, and particularly, extracting general insights from historical data. ML provides a set of tools that allows, among other things, to automate the task of obtaining a demand curve for a product based on its properties. And furthermore, you get "in one go" the measure of similarity of products. Similar products can "inherit" or "share" each other useful historical information about demand as function of price and other factors. This inheritance and similarity are established through the feature space, the abstract space where our products "live". A product properties and context information are mapped to features, a list of numerical values, which represent a point in the feature space. The task of mapping product properties to features is one of the primary responsibilities of an ML engineer. Training an ML model can be viewed as inferring a measure of similarity in the feature space.
There's a common argument that many products lack sufficient data, which supposedly makes it impossible to define a demand curve for them. While this can be the case, this argument requires clarification. The quality of predicting the demand curve of a product X depends not only on the personal historical data of product X's sales but also on the amount of historical data for various products that map to the same feature space region as X. Therefore, even if a product has no available sales data, an ML model can still predict its demand curve as long as there are neighbours in the feature space.
Consider the table with historical data in the form of table with date, price, features and sales:
|
|---|
Basically, it is a standard ML task to predict one column of the table based on the other columns. Thus, you can train a model to predict sales based on product features. For prediction, you input into the model a similar table but without the "sales" column, and the model will generate this column with predicted values. By selecting a single row from this table and substituting various values into the price column, you can obtain different sales values, which together form the predicted demand curve for a specific product. The features can be product properties like category, average number of sales in the last month, competitor price on that day, as well as day's properties (day of week, days left to black Friday) or discount properties (min bucket price, min quantity, etc).
Features are the key to the problem; they form feature space where patterns and generalizations are sought. Price is also a feature, but a special one since it is considered as a variable that we manually vary for demand curve forecast.
Why it is not that simple
There are several complex issues to consider when training a demand curve. For example:
Different elasticities for different types of promo. Each promotion mechanism (discount, promo code, cashback, coupon) can have its own curve. More precisely, each combination of factors, related to marketing and beyond, can have its own curve (recall mentioned visibility, expectation, clarity of a promo).
If discounts are accompanied by some additional promotional efforts (TV advertising, performance and display web ads, storefront displays, app push notifications), the elasticity is largely determined by the quality and scale of this promotion.
Long-term and short-term curves E(r) can differ. Price changes might not affect sales immediately but could do so after a few months.
Addressing these issues is no simple task, and we won't be covering them in this article.
Preparing data for training
Data cleaning
As always, careful data preparation is crucial. This involves verifying its reasonableness and cleanliness, and removing any potentially misleading "samples". Specifically, it is reasonable to exclude the following from the training data set:
OOS (out of stock)
clearance sales of remaining stock
dead seasons (e.g. fur coats in the summer)
and, generally, any outliers in a specific product's sales time series – unusual deviations both upwards and downwards
Seasonality
The next challenging aspect is seasonality. Sales changes are sometimes related to seasonality, and we want ML not to attribute them to the price in cases when the start or end of a season aligns with a price change.
There is an approach based on adding seasonal multipliers to different product categories, but it is not effective and can not be accepted as a systematic solution. Accounting for seasonality seems to be a complex task, and despite being quite noticeable and predictable at the category level, it does not work at the level of individual products. A product that performed well in one season is likely to be replaced by an analogue in the next. Seasonal multipliers vary significantly between products of the same category and do not repeat year after year. However, when it comes to training a normalized demand curve, seasonality becomes less significant. As will become clear, the optimal price is determined by the normalized demand curve, and the absolute demand values are not so important (although they are important for replenishment). One straightforward way to account for seasonality is to add the "day of the year" feature, but this can lead to overfitting. Overfitting is a model degradation when it starts to memorize historical data instead of inferring general insights. The "day of the year" is a leaky feature that helps such memorization. Protection against overfitting may involve adding special regularization of this feature by noising it during training or reducing the number of layers and their size in a special "short and thin leg" of the neural network. Specifically, the architecture of your neural network could include a separate section, often referred to as a "leg" or "tower", where such leaky features like the "day of the year" can be fed in. We will delve deeper into this later.
Why we need context features
In general, the discussion of seasonality brings us to an important understanding of the need for a multi-feature model. We want the model to be able to attribute sales movements to factors other than price changes, such as:
seasonality, holidays
changes in weather
retail events
actions of competitors (reference prices)
marketing activity (yours or competitors')
Therefore, it is useful to add features corresponding to these phenomena so that they can "explain" some of the sales movements, and as a result, when considering dependence on the price feature, a clean, correct elasticity remains. We refer to this as context features sales attribution.
Features related to the context rather than product itself are called context features. Notable context features include competitor prices and the number of days leading up to or following a retail event. But you should be careful with these features as they can be the source of overfitting and pitfalls.
Price leakage
Thus, we have concluded that it is important to include context features that correspond to various phenomena to account for certain sales movements. This ensures that the elasticity of demand with respect to price remains accurate and unaffected by other factors. However, adding certain features, such as price_yesterday, can lead to a leakage of information about the price variable. This occurs because the price from the previous day is often the same as today's price, leading the ML algorithm to potentially misattribute the relationship between sales and price to the previous day's price. More intricate leakage scenarios can occur when using features like the sales vector for the past 14 days. In this case, a drop in sales yesterday may be caused by an increase in price yesterday, and the ML model may infer this causality. And then we have the same leakage, as a high price yesterday often corresponds to a high price today, making the price feature not the only source of information about todays' price.
Simple regression
Let's choose any product and look at prices and sales for the last N days. As a result, on the plane (log(price), log(sale+1)), we can obtain a "cloud" of N points. Our models have predict = log(sales + 1) as their output, rather than sales, and predicted sales are calculated using the formula max(0, exp(predict) - 1). We call this the target_transform, that is the forcing models to predict a nonlinear function of sales, rather than sales themselves. We tested various target_transforms and this one is simple and exhibits stable prediction quality.
Next, we can attempt to fit a straight line through this cloud of points, solving the standard regression problem of minimizing the sum of squared residuals. This approach already gives a more or less acceptable solution.

But in this approach, it is especially important to perform what we referred to earlier as "data cleaning" (removing OOS, dead seasons, clearance sales, etc.).
The next important step is to use not a straight line, but, for example, a sum of sigmoid functions
where , and
are some parameters, predict = log(sale+1), and x = log(price).
But replacing linear regression with parametric regression is a half-hearted solution. Indeed, the "sum-of-sigmoids" model enables a variety of curves on the plane (f(price), g(sales)), but it still falls short in addressing the aforementioned context features sales attribution. While neural networks can address this and some further challenges.
The features
Here is our list of feature groups:
Sales and price features for the last N days aggregated in different ways (window averages, exponential averages, etc.).
Correlations between sales and prices for the last N days.
Competitors' prices.
Product and category embeddings.
Information about promotions (if there was any additional promotional activity beyond discounts).
Seasonality.
Average delivery time.
The "Correlations between sales and prices for the last N days" feature is particularly interesting. Suppose you have the average price per day and sales per day
for the last N=42 days,
. Then you can calculate
for different u and v. Each pair of u and v yields a factor. Instead of exponents, you can take other non-linear functions of sales and price, such as logarithms.
Feature set preparation may significantly impact the quality of the result. You should decide what data you use as input to your model and how you map this data to set of features. Mapping data to features usually means cleaning, calculating aggregated values, applying different transformations.
My personal "alchemy toolset" consists of the following
Make utmost features dimensionless, for example:
instead of the average price for n=7 days use the normalized logarithmic feature log(avg_d7_price / price0)
instead of the average sales for n=7 days use the normalized logarithmic feature log(avg_d7_sales / demand0)
price0 and demand0 could be defined as average price and average demand per day for a long period, for instance 28 days.
instead of SD (Standard Deviation) for a series
use dimensionless
If a feature has specific units (such as currency or sales units), I take its logarithm. Minimize number of features measured in currency or counters. Be aware of them and reason yourself why you use them.
If a feature can be rid of noisy and incident-affected data, it's advisable to do so. For example, average sales over 42 days can be made as the average sales over 42 days on clean days, where clean days stands for no clearance sales, no OOS, and the point is not an outlier in the 42 days series of sales.
f a feature seems difficult to clean, then provide the necessary data as features, allowing the neural network to handle the cleaning on its own. For example, you can provide a vector of daily sales data for the last 14 days, as well as a vector with information about whether the product was in stock for each of those 14 days. But as I mentioned earlier, providing data about sales in previous days carries risk due to the potential leakage of price change signals, so in our case, it is reasonable to do cleaning manually.
Filtering Stability Periods
The next important stage is removing 98% of random rows from the training dataset where the price varied by less than 5% from the 42-day average price. This data manipulation underscores our interest in instances of price change, prompting the model to focus more on these changes rather than predicting demand on days with stable prices.
Neural Network Architecture
The neural network architecture we came up with is very simple and essentially the following:
The number of layers is 9, with an average layer size 15
The number of input factors is approximately 70, and they are normalized, so that
mean = 0, std = 1The target was transformed using the formula transformed_target = log(sales + 1)
The size of the train dataset ranged from 4 million to 20 million (we trained models for selected assortments, so train dataset sizes vary)
One residual connection is added
A couple of LayerNorm layers is added
Some features, including price, categorical features embeddings, and the "day of the year" feature are fed into special independent "leg", called Elastic encoder, which is short and thin.
Batch size is from 2000 to 8000 at the last epoch.

The Dynamic features encoder (the left leg) has the following code (class DemandNet1):
import torch
import torch.nn as nn
class DatasetNormalization(nn.Module):
"""
Just add this layer as the first layer of your network
and it will normalize your raw features.
But do not forget to take log of counters-like features by yourself.
"""
def init(self, x, nonorm_suffix_size=0):
super().init()
mu = torch.mean(x, dim=(-2,))
std = torch.clamp(torch.std(x, dim=(-2,)), min=0.001)
if nonorm_suffix_size > 0:
mu = torch.cat((mu, torch.zeros(nonorm_suffix_size)))
std = torch.cat((std, torch.ones(nonorm_suffix_size)))
self.p_mu = nn.Parameter(mu, requires_grad=False)
self.p_std = nn.Parameter(std, requires_grad=False)
def forward(self, x):
return (x - self.p_mu) / self.p_std
class DemandNet1(nn.Module):
"""
This network is the first to try.
+ DatasetNormalization
+ Some Linear + ReLU, one LayerNorm inside
+ one residual connection
"""
constants = ['output_size']
def __init__(
self,
x_norm_prefix, # train_dataset without embeddings,
# for DatasetNormlization layer initialization
mid_size: int = 20,
embed_size: int = 0,
output_size: int = 1,
activation: nn.Module = nn.ReLU()
):
super().__init__()
input_size = len(x_norm_prefix[0]) + embed_size
self.norm = DatasetNormalization(x_norm_prefix, embed_size)
self.output_size = output_size
self.leg = nn.Sequential(
nn.Linear(input_size, mid_size),
activation,
nn.Linear(mid_size, mid_size),
nn.LayerNorm(mid_size),
activation,
nn.Linear(mid_size, mid_size),
activation,
nn.LayerNorm(mid_size)
)
self.body = nn.Sequential(
nn.Linear(input_size + mid_size, mid_size),
activation,
nn.Linear(mid_size, mid_size),
activation,
nn.Linear(mid_size, output_size)
)
def forward(self, x):
x1 = self.norm(x)
x2 = self.leg(x1)
x = torch.cat((x1, 4 * x2), dim=1)
yp = self.body(x)
return torch.squeeze(yp) if self.output_size == 1 else yp
In principle, you can use a one-legged architecture (the DemandNet1 as one leg sitting on all the features), and this yields results that are comparably good according to metrics.
We use two-legged architecture with the special right leg, the Elastic encoder, sitting exclusively on the price feature, categorical features embeddings, and the "day of the year" feature. This approach allows us to control demand curve regularization. The Elastic encoder can be defined as k-parametric family of normalized demand curves E(r, p1, p2, ..., pk) (for instance, sum of several ReLU functions). The first layers of right leg output k parameters (p1, p2, ..., pk), and then the node log_mul = log(E(r, p1, p2, ..., pk)) follows next. The encoder variant with k = 9 provided us with the best offline metrics values. The parametric curve can be strictly monotonic by definition. The demand curves provided in the first section were obtained not through a monotonic family. And among them there are non-monotonic ones, and even one with a slope at r = 1 not in the right direction, but they can be transformed to monotonic smooth curves using post-processing.
Sometimes you may want to predict not just one day's sales, but a vector of sales for M days: sales in K-th day, (K + 1)-th day, ...,(K + M - 1)-th day. Accordingly, a network should output a tensor with dimension M, and your loss function should calculate mean error for all values in the tensor.
We use embeddings for feeding categorical features to our network. These features are sku, sku_leaf_category, sku_level_1_category, normalized_sku_name, price_class, demand_class; and you can guess their meaning from their names. These 6 identifiers were "embedded" into a low-dimensional space (with 2, 3, 4, or 5 dimensions) and together they gave an additional embed_size = 20 features.
For the transformed_target, you can use the MSELoss as the loss function, but a slightly modified SmoothL1Loss does a better job. It is defined as a quantile loss for 65%-quantile with a smoothed peak as zero:
import torch.nn as nn
import torch.nn.functional as F
class SmoothQLoss(nn.L1Loss):
constants = ['reduction', 'beta', 'qx']
def __str__(self):
return f"{self.__class__.__name__}(beta={self.beta}, qx={self.qx})"
def __init__(
self,
size_average=None,
reduce=None,
reduction: str = 'mean',
qx: float = 0.5,
beta: float = 0.1,
):
super().__init__(size_average, reduce, reduction)
self.beta = beta
self.qx = qx
def forward(
self,
predict: torch.Tensor, target: torch.Tensor
) -> torch.Tensor:
m = 2.0 * self.qx - 1.0
shift = self.beta * m
if self.reduction == 'mean':
return (
F.smooth_l1_loss(
target - shift, predict, reduction='mean',
beta=self.beta
) + m * torch.mean(target - predict - 0.5 * shift)
)
elif self.reduction == 'sum':
return (
F.smooth_l1_loss(
target - shift, predict, reduction='sum',
beta=self.beta
) + m * torch.sum(target - predict - 0.5 * shift)
)We use parameters qx=0.65 and beta=1.0.
Quality Metrics for Demand Curve Prediction
While experimenting with features, network architecture, and hyper parameters, it is important to have a simple offline metric that indicates whether a change is beneficial or not. We tested more than 10 different approaches for this metric and finally, we came up with the metric known in Catboost as QueryRMSE.
We use a pair of categories (product category, product price category) as a group identifier, and, as previously stated, the target is y = log(sales + 1).
The idea is for each group to seek a constant additive correction a(group) that minimizes the mean square error between ytrue = log(fact_sales+ 1) and ypredicted = log(predicted_sales+ 1):
and then the obtained minimized values of errors in groups are averaged, possibly with some weights:
This metric, unlike the standard MSE, places less emphasis on the error in absolute values and focuses more on errors in the normalized demand curve. The corr_mse metrics literally "forgives" systematic additive errors in groups.
But additive error for y = log(sales + 1) corresponds to multiplicative error in predicting the value of sales + 1. That is, if we make a mistake of a factor of two in our forecast for all products in a group, this metric will "forgive" us. In other words, this metric measures the accuracy of predicting the ratios of sales values among different SKUs within a group, rather than the actual sales values themselves.
ML Pipeline
There are crucial aspects that cannot be overlooked. The key to successful ML research and shipping ML-models to production is always an end-to-end validated pipeline. This pipeline should start with collecting datasets from raw data, do all necessary data transformations, train selected models, evaluate predictions on the test dataset, calculate metrics, and add them to the results table. It's vital that pipeline is:
From raw data to a leader board sorted by a single ultimate metric (this eliminates disputes over which model is the best one)
Reproducible (otherwise, it lacks credibility)
Fast (from idea to result verification is 1 day or less)
Bug-free (just a dream)
Equipped with "ship it!" and "unship it!" buttons (to enable deployment and rollback without hassle).
Profit Maximization Problem
When you have a demand curve, you can explicitly solve the profit maximization problem. Let's simplify picture by omitting some tax-related aspects, and write down the formula for profit:
Here, additional notations were introduced:
The "cost" itself includes the purchase price, operating costs, and other associated expenses. The most accurate general definition for our purposes is the following:
Cost is what needs to be subtracted from the price to obtain something proportional to profit.
Let's introduce the relative profit function:
The profit maximization problem essentially boils down to finding the price r that maximizes P(r).
Let's consider an example.
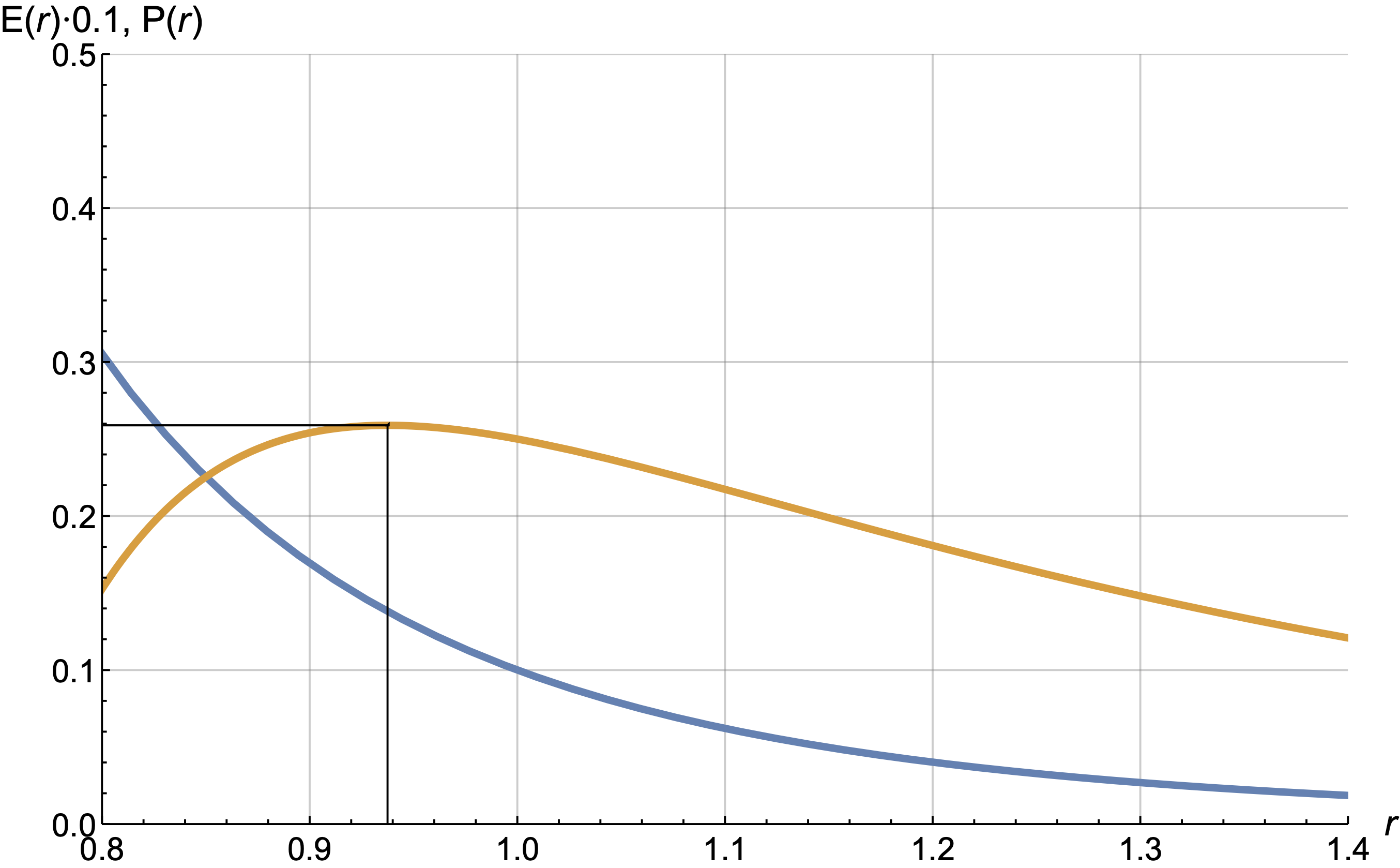
The profit graph (yellow) has a maximum somewhere around 0.94, meaning to maximize profit, the price0 should be reduced by 6%. For the power curve , the profit maximum is achieved for the price:
We will further derive this formula for the more general case of conditional profit maximization.
Profit vs GMV balance problem
Yandex Market's task is not a profit maximization problem. Total sales and price perception are important, as they correlate with future profit. To simplify the situation greatly, the task is close to balancing between two metrics – GMV and Profit.
And when it comes to balance, the Lagrange multiplier method inevitably appears.

The Lagrange multipliers method applied to our case looks like this:
Problem 1: Maximize
subject to the condition that
under certain conditions can be replaced by
Problem 2: Maximize
with some λ.
The point is that each solution of the second problem provides an answer to the first problem for some value of . You just have to guess the correct λ to hit the right
, and note that some values of
are not reachable. Strictly speaking, Lagrange himself considered only the case of equality constraints, that is, for our task
. And in practice for typical curves and positive
we achieve this equality. The case of inequality conditions was worked out by other mathematicians, see Karush–Kuhn–Tucker conditions for clarification.
Interpretation of λ
The number λ has a simple interpretation. Each λ gives a point on the plane (gmv, profit). These points together form a navy blue curve on the graph below.
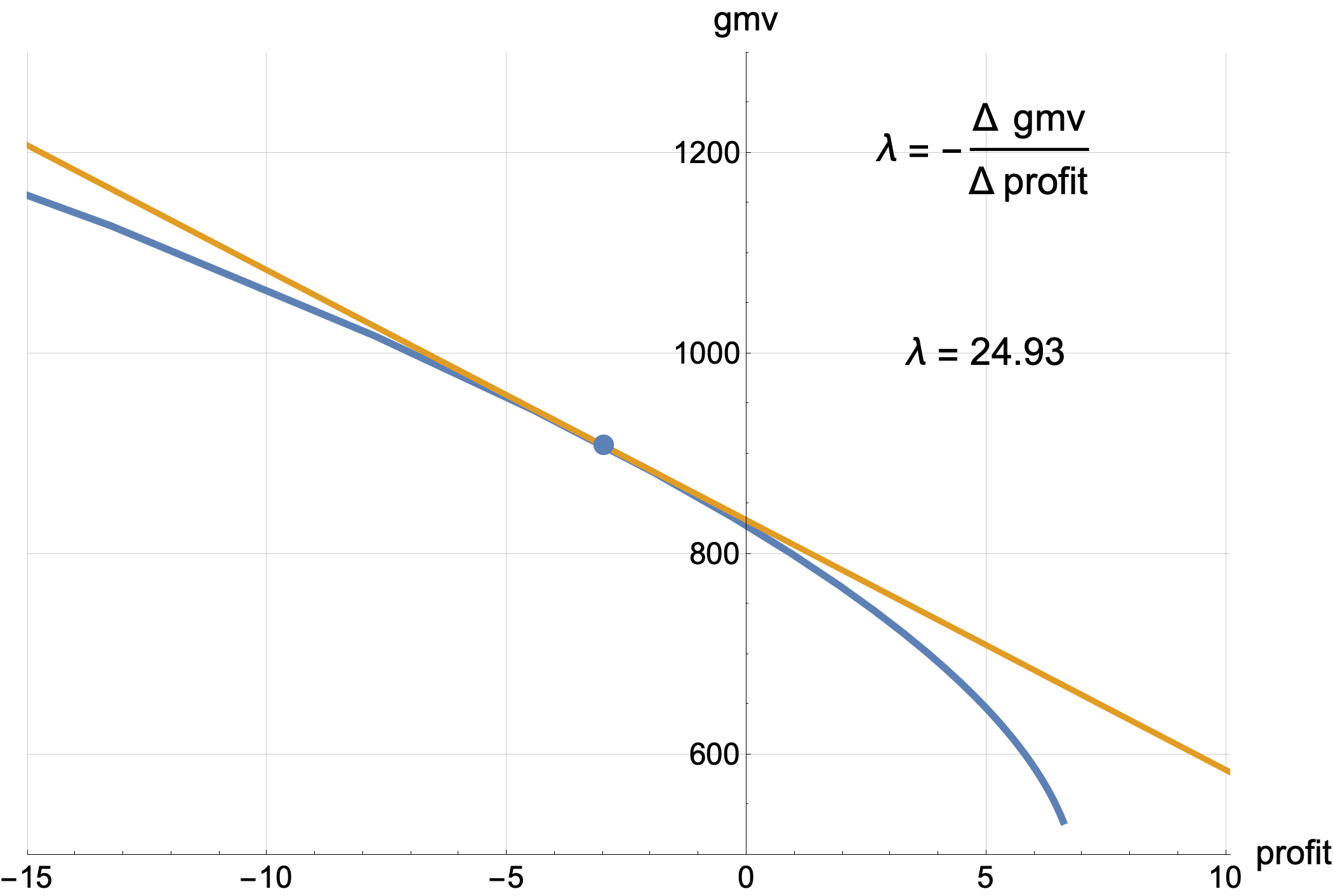
The yellow line is the tangent to the navy blue curve at the given point. The slope of tangent line is -λ.
You just need to guess such a value of λ, so that the tangent line with slope -λ just touches the point with the profit value you need.
There's an alternative perspective, arguably more accurate, where the primary focus is on the value of λ, not the profit constraint P0. Give me a try to convince you. If you aim for a certain profit every day, you end up with a unique λ each day. However, having different λ values on two consecutive days is not optimal. Why? Let's consider an analogy. Suppose you buy tomatoes at the market every day, and the sellers there operate in such a way that the more tomatoes you buy from them, the higher the price they set. Each subsequent tomato is slightly more expensive than the previous one. This is why you need to go to the market every day, as prices are lower in the morning and then increase. The tomatoes don't spoil, and you could bulk buy for a long period, but unfortunately, the price for a large quantity in one day is high. If you ended up buying the last tomato yesterday for $0.10, and today for $0.15, you acted inefficiently, because yesterday you could have bought a couple more for just over $0.10, and today you could avoid buying the last tomatoes for $0.15. The value of λ is the price of the last tomato you bought. And a tomato represents $1 of profit that you buy for $λ of GMV.
Of course, it's easier for a business to think about a specific profit value and the cash that's crucial to have each month to cover planned expenses. But the optimal solution is to somehow magically guess the value of λ and keep it unchanged for a long period, or only slightly "adjust" it, like changing λ by a couple of percent or less once a week.
One feasible strategy is operating with slightly increased value of λ, and having marketing channels for fast exchanging excess profits to GMV with a good exchange rate. These excess profits could be considered as additional variable budget for high scale promotional campaigns.
Optimal price formulas
Let's consider three families of curves. They are parametrised by one parameter s.

Lagrange method gives the following answers:

The optimal values of r are denoted in the following pictures with dashed lines.
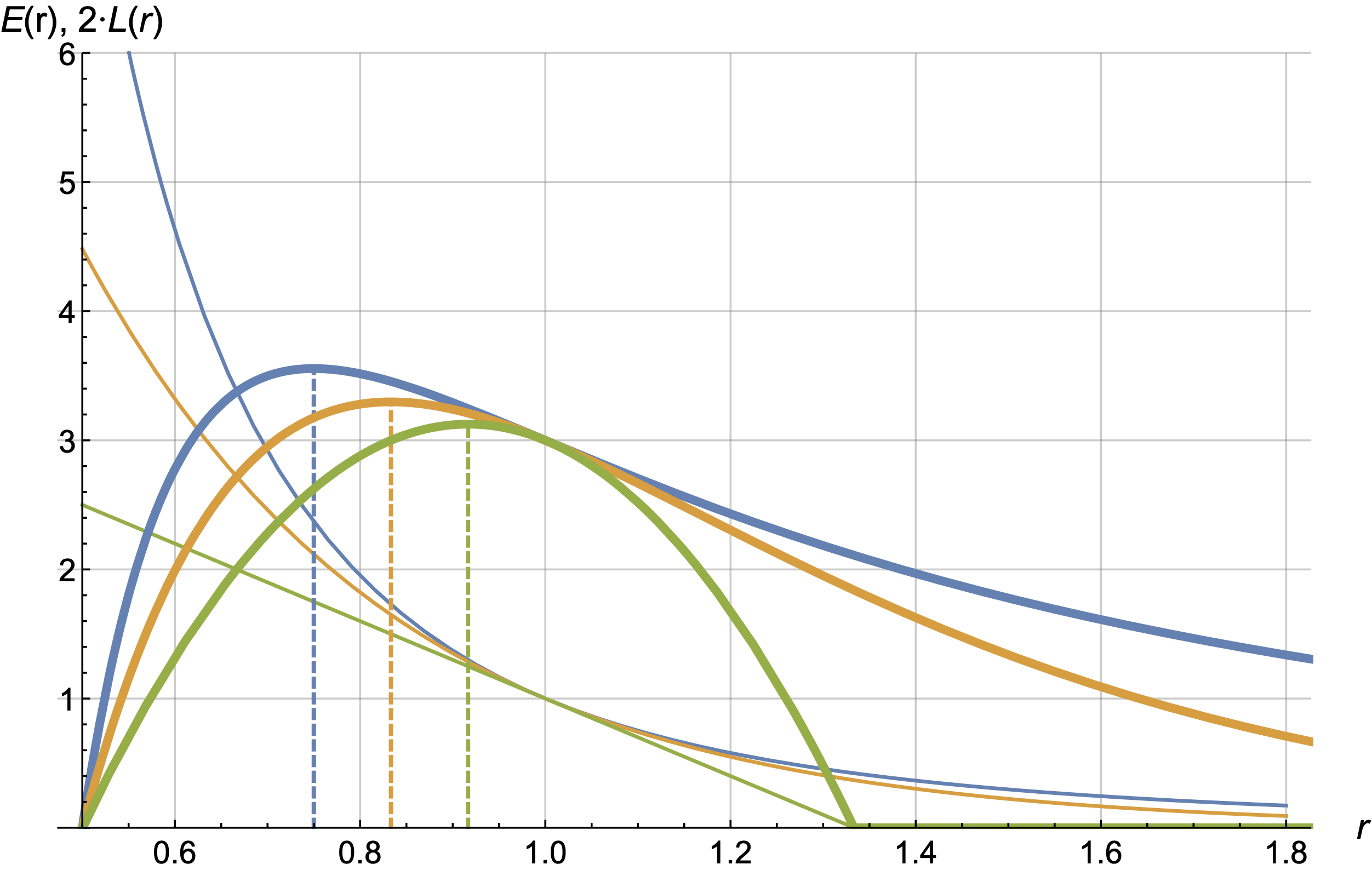
Let's discuss the first (blue) case as the most typical one.
The derivation of the formula is straightforward application of Lagrange multiplier method. Consider the Lagrangian function:
Take its derivative by r and equate to zero:
Substituting we get
After simple transformation you get the answer:
Lets look at the resulting formula. When , the price should be exactly the value of c. We won't make any profit on the sales of this product. If
, the price will be less than c, and we will lose profit on this good (which is absolutely correct), and on goods with
we will make a profit.
When the elasticity is low and approaching 1, the formula suggests setting an arbitrarily high price. This is due to the fact that the power curve does not quite correctly describe the range of high prices, and this needs to be taken into account. The simplest way to fix this is to do the following:
add an exponential decay multiplier to E(r) for r grater than some threshold value rt
search for the maximum L numerically
The Pricing algorithm
The optimal value of is one for all products. The P0 constraint is a restriction on the total profit across all products.
In this formula, values of gmv0, rλ, E(rλ), and c are sku-wise.
The algorithm in a nutshell can be stated as follows. Set λ = 5. If the profit seems small to you, increase λ to 7. If it's still too little, then increase it to 10. If you like the profit, then you can gradually decrease λ to increase sales and win the market. Continue applying small changes to λ balancing between GMV and profit according to current needs and strategy of you business.
More formally it can be stated like this:
Step 0: Select initial λ = 5. Select fixed global stability parameter
.
Step 1: Select/update value of P0 according to business needs and strategy.
Step 2: For current λ calculate prices, and find out what a
is.
Step 3: If
, slightly increase λ.
If, slightly decrease λ.
Change in λ in a week should be no more thanpercent.
Go to step 1.
Steps 1, 2 and 3 can actually be de-looped during preliminary stage. One can simply shoot a hundred variants of λ and using model predictions choose one that gives preferable values of GMV and Profit. The loop here is introduced for real life setting, when you have regular updates of business needs and strategy, and model predictions. You need to constantly look for segments where the model predictions are not that good, and improve the model by adding more features or/and changing training approach and dataset.
Takeaways
Successful ML for predicting demand curves prerequisites:
Careful data preparation (otherwise garbage in – garbage out).
Context features (so that the model can attribute sales movements not only to the price feature).
End-to-end validated ML pipeline (to test hundreds of models and select the best).
Neural networks provide a mature and actively evolving toolset to achieve acceptable model quality and fight pitfalls.
Optimal price:
Lagrange method do the job of balancing among several KPIs (GMV, Profit, ..).
The insightful and quite applicable in practice formula of the optimal price is:
.
Success = ML + Human expertise + Analytics.
ML engineers can train E(r).
Experts can indicate how to influence E(r), point out some pitfalls and inconsistencies of forecasts and expectations, help to improve the model by eliminating some errors, outline scopes of applicability of formulas.
Analysts can make honest A/B-evaluations of pricing algorithms, find mistakes, and draw accurate, statistically justified conclusions.
PS: please feel free point out errors (in english, or math) in private messages.
